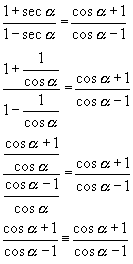GTmetria :): Revisa nuestros ejercicios!

EJERCICIOS DE GEOMETRÍA PLANA
A conticuación vamos a poner en práctica lo que hemos aprendido en clase, al revisar los teoremas teóricamente ahora resolveremos algunos ejercicios.

1. Hallar el valor de los ángulos internos de los siguientes polígonos regulares

a) De un pentágono: para resolver este ejercicio, ponemos en práctica el Teorema 33 que dice:

"La suma de los ángulos internos de un polígono es igual a dos rectos multiplicado por el número de lados del polígono menos dos"

Resumiendo tenemos: 180° (n-2)

Para el pentágono solo reemplazamos el lado de lados que tiene un pentágono, es decir 5 lados en lugar de n y así tenemos:

= 180° (5-2) = 540°

2. Hallar el valor de cada ángulo de un polígono regular.

b) De un pentágono: para hallar el valor de cada ángulo del polígono, igual que el ejercicio anterior utilizamos el teorema 33 pero ahora utilizamos la fórmula arreglada justamente para este tipo de ejercicios:

Resumiendo tenemos: 180° (n-2)/n en esta fórmula sólo cambia el hecho de que tenemos que dividir todo para el número de lados.

Para el pentágono solo reemplazamos el lado de lados que tiene un pentágono, es decir 5 lados en lugar de n y así tenemos:

= 180° (5-2) = 540°/5 = 108°

3. Cuántos lados tiene un polígono que en cada ángulo vale 7/4 rectos.

c) Para este ejercicio sólo tenemos que razonar y relacionarlo con los dos anteriores, de esta manera tenemos lo siguiente:

7/4(90°) = 180° (n-2)/n

157,5n= 180n-360n

n= 16 lados.

EJERCICIOS DE LA SUMA Y RESTA DE ÁNGULOS

EJERCICIOS DE IDENTIDADES TRIGONOMÉTRICAS
En base a las fórmula que ya hemos revisado puedes revisar los ejercicios realizados por nuestros compañeros:

1. Demostrar:

2. Demostrar:

3. Demostrar:

EJERCICIOS DE LA RESOLUCIÓN DE TRIÁNGULOS OBLICUÁNGULOS

1. De un triángulo sabemos que: a = 6 m, B = 45° y C = 105°. Calcula los restantes elementos.

2. Resuelve el triángulo de datos: a = 15 m, b = 22 m y c = 17 m.

EJERCICIOS DE TRANSFORMACIONES GRÁFICAS DE LAS FUNCIONES TRIGONOMÉTRICAS

Esta vez te dejamos con un ejemplo para que te des cuenta de como aplicamos la Transformación Gráfica de las Funciones Trigonométricas:

Gráfica de la función y = -3sin(2x- π /3).

Amplitud = |-3| = 3

Período = 2π/2 = π

Desfase = π/6